Neetcode Data Structures and Algorithms for Beginners

Summary: Neetcode is a course designed to help you master algorithm-style coding interviews.
The course takes you through data structures as well as some of the core algorithms involved in leetcode-style problems.
I thought the course was great, but wish that there were more of a focus on Javascript/Typescript as well as more coverage of how to generally tackle problems, rather than simply explaining the most optimal solution.
Rating: 8.5/10
Arrays
- RAM
- Whatever information we're trying to store gets stored in RAM
- RAM is stored in bytes
- A byte is 8 bits
- A bit is a 0 or a 1
- Every value in RAM is stored at a distinct address
- Every value in an array takes up 4 bytes
- Arrays are the simplest data structure. They are stored at contiguous addresses in memory
- In a string, each character would take up just 1 byte
- Static Arrays
- If you've allocated a certain amount of RAM for an array and then go to add a value at the end of the array, you would not be able to do so
- A static array has a certain, limited size
- Think about the way that this data gets stored in memory. That is why it is easy and efficient to push to an array, but not to add in a new first value
- Dynamic Arrays
- These are what gets used in javascript and python, for example
- The size is not specified
- For the RAM that is allocated, once you exceed the initial amount allocated, memory will allocate a new larger chunk of memory (double the size of the previous), copies over the values, and then deletes the values stored at the old location in memory
- Stacks
- Supports 3 methods: push, pop, and peek/top
- Push = O(1), Pop = O(1), Peek/top = O(1)
- A stack can be implemented using a dynamic array
- It can be easiest to visualize a stack as vertical and think of adding/removing/looking from the "top" of the stack
Linked Lists
-
Singly Linked List
- A singly linked list has ListNodes that have a value and a next property
- Pointer: A pointer is a variable which holds the address of other variable of the specified data type(like int,float,char). In programming we basically use pointers to store the other variable's address.
- Consider just having Nodes with values that are not connected. You need to connect them or "wire them up" by pointing the next properties to the proper Nodes. The next pointer is telling you that the address is the address of the object
- In order to loop through a linked list, you can do the following:
let cur = ListNode1 while (cur !== null) { cur = cur.next; }- Unlike arrays, you can remove a single element in constant time by doing node.next = node.next.next. That would mean that node.next was effectively removed.
-
Reversing a linked list
- Two pointers
- Start with prev as null, curr as head
- Update next to prev
- Set prev to curr, curr to next
- Once curr = null, then you're done and you can return the head, which is prev
-
Doubly Linked Lists
- In a doubly linked list, the ListNode has a value, plus a tail and a head
- It also has a head and a tail
-
Queues
- FIFO = First In First Out. First element that we add is going to be the first element to be removed
- Enqueue, Dequeue
- Enqueue -> pushed to the end of the queue
- Dequeue -> removed from the beginning of the queue
- Queues generally get implemented with linked lists, but can be done with arrays
Recursion
- Factorial
- Break one problem into smaller sub problems that are done the same way
- Factorial looks like this:
- n! = n*(n-1)(n-2)(n-3)...1
- If you're computing 5 factorial (5!), you know that you can break down the first problem as 5 * 4!
- So the recursive step is n * factorial (n - 1)
- Then consider the base case, which is basically the last step of recursion
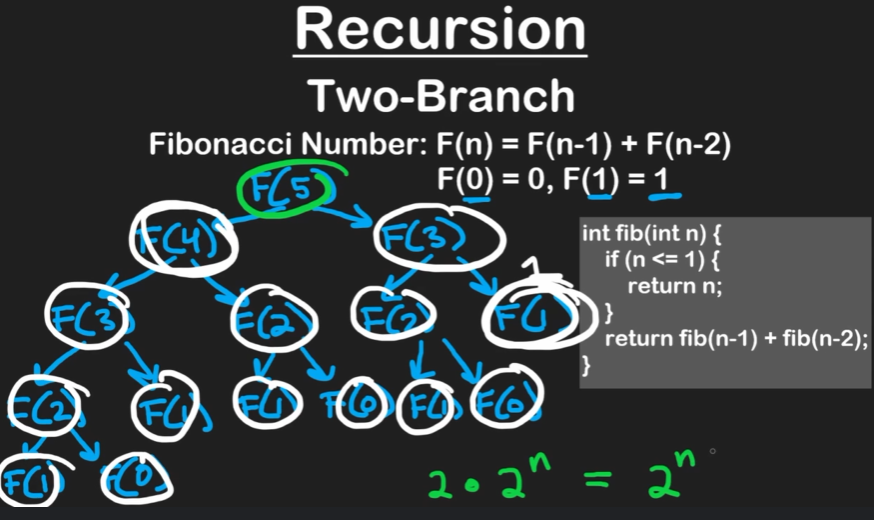
- Two Branch Recursion
- Fibonacci is a good example of two branch recursion, where in order to get f(n), you need to add f(n - 1) + f(n - 2)
- At each level, we split off the hypothetical 2 decisions we could make
Sorting
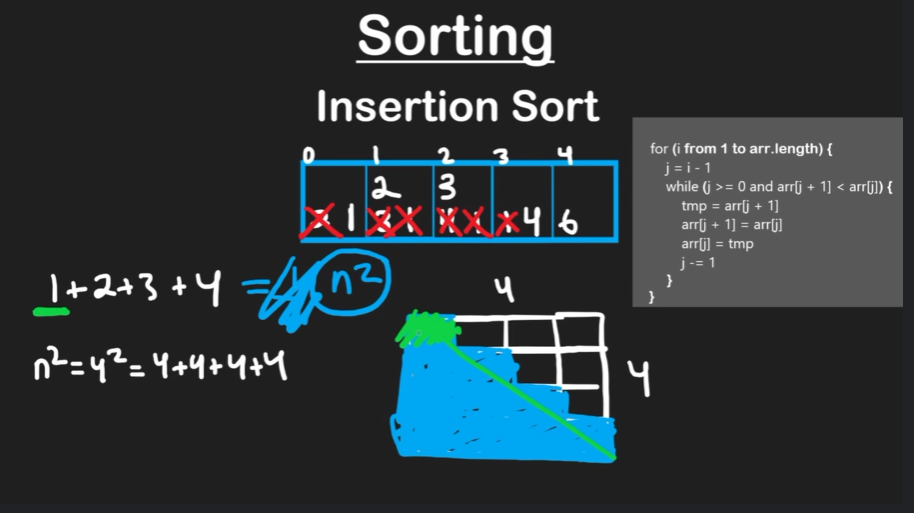
- Insertion Sort
- Break the problem into sub problems
- Any array of 1 value is considered sorted
- Iterate through and compare the value to its left neighbor. Swap if needed
- You will always know that everything to the left of your value is sorted
- The best case time complexity is O(n)
- The worst case time complexity is what matters for time complexity though. In insertion sort, the worst case time complexity is O(n^2). This is because the worst case can be approximated as 1/2 * n^2. And if you drop the constant, that is O(n^2)
- Merge Sort
- Take the input array and split it in half
- Then take the next input and split that in half, so on and so on until you end up with arrays of single elements
- The problem naturally lends itself to recursion
- It is 2 branch recursion, since you are splitting into two branches each time
- Divide and conquer is the name of the technique - divide the problem into sub problems and solve
- When you go to combine the arrays back together, you take two pointers: one at the first element of array 1 and one at the first element of array 2
- The time complexity of merge sort is O(nlogn)
- Quick Sort
- Quick sort is similar to merge sort
- Rather than continually splitting the value into halves, we pick a pivot value
- Every value less than or equal to pivot goes to left, every value right of the pivot goes to right
- No extra memory needs to be created to partition the arrays
- You need two pointers
- At each value, you check if its less than or equal to the pivot (which is often the last value in the array)
- If it's not less than or equal, the value stays
- If it is, then it's placed to the left of the values that are greater
- The worst case is O(n^2), but the average is O(nlogn), so it is generally considered an O(nlogn) time complexity algorithm
Binary Search
- Search Array
- Can only run on an input that is already sorted
- In the worst case, to look for something, you would look at every value -> O(n)
- Intuitively though, we know that in a sorted array, we can look at the middle, check if it's lower or smaller, then keep repeating that until we find the value
- Search Range
- Rather than finding a target, one version of this problem is to search for a number that satisfies certain conditions
Trees
- Binary Tree
- In a binary tree, there is a child/parent relationship
- Each parent has up to two children
- Binary Search Tree
- Same as a binary tree, but sorted. The left child must be smaller than the parent and the right child must be larger
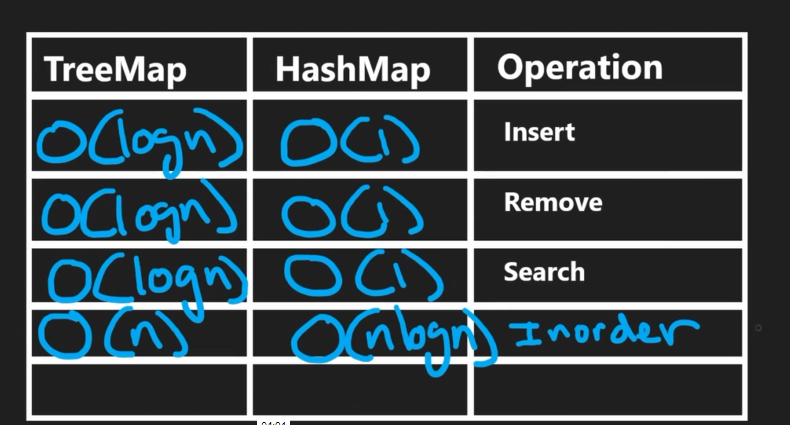
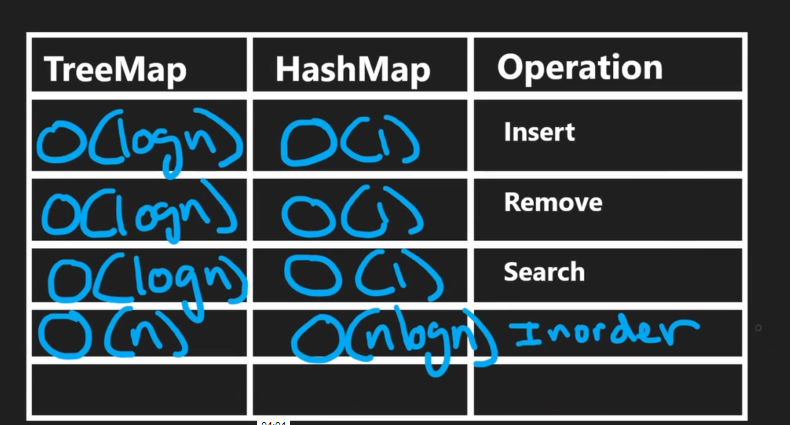
- The main benefit of BST's is that you can insert and remove nodes in O(logn), which is different than doing so in an array, for example
- BST Insert and Remove
- Keep going through and looking to the left if smaller, right if larger
- Once you find an "empty" spot (where the left or right value is null), insert the node there
- When replacing a value that has two child nodes, it is best to search through and replace it with the smallest value in the right sub tree or the largest value in the left sub tree
- Depth First Search
- In order to go through the tree in sorted order, you will need to go left to right
- BST Sets and Maps
- Set: only unique values
- Map: keys get "mapped" to values
Backtracking
- Try a particular path. If that path does not work, backtrack and try another path until you recursively try every path
- Then, if true, start returning true all the way up the chain of recursion
- For backtracking where you're keeping track of values, ensure that you remove (pop in the case of arrays) from the array once you find that you're on the wrong path
Hashing
- Hash Usage
- Sets are a set of values
- Maps are a set of keys that are mapped to values
Heap/Priority Queue
-
You can prioritize the values based on minimum or maximum -> minimum would mean that you would start popping with the smallest value, then next smallest, etc.
-
A priority under the hood is implemented as a heap
-
A binary heap is a heap where each parent has up to 2 children - and they are placed to the left and right
-
Structure property: a binary heap is a binary tree that is considered a complete binary tree. Every level in the tree is completely full, except possibly the lowest level. This is a requirement of heaps.
-
Order property: for a minimum priority queue, every value to the left and right must be greater than the root. This is recursively true at every level of the tree.
-
The entire point of having a priority queue is to find the minimum value or the maximum value super easily.
-
In the case of the above minimum priority queue, we can find the minimum value in O(1) time. It is the root node
-
While we visualize binary heaps as trees, they are implemented under the hood as arrays.
-
We do not use index 0 in the array. Index 1 is the root value.
-
Then, going left to right, in a breadth first form, we start filling in the next values
-
We skip index 0 in order for the math to work out. With this setup, the following are true:
- leftChild: 2*i
- rightChild: 2*i + 1
- parent: i / 2 (and round down)
- So to get the left child's index in that array, you multiply the index times 2, right child you multiply index times 2 and add 1
- Note that those rules are only true due to it being a complete binary tree
-
Push and Pop
- Push: If placing in a new value (pushing) that is not the lowest: start with the spot that happens to currently be in order. Compare to its parent. If less, swap them. Continue this process until the value is in place.
- Comparison with the value is done via getting parent value in terms of the array value (see above). If parent, look at Math.floor(i/2), for instance
- Pop: Need to maintain structure and order properties. If you remove a node and move appropriate other nodes up, you can introduce holes.
- The real way to do it is to remove the value, replace it with the very last value in the array (which will then not satisfy the order property). Then you start percolating down, swapping with values below if you find that it's lower.
-
Heapify